聚类分析

Posted on 2020-05-30 Edited on 2021-07-25 In 机器学习 , 聚类

机器学习—聚类篇

1.聚类算法的概述:

聚类试图将数据集中的样本划分为若干个通常是不相交的子集,每个子集对聚类算法而言,样本簇亦称”类”称为一个”簇” (cluster). 通过这样的划分,每个簇可能对应于一些潜在的概念(类别) ,

聚类既能作为一个单独过程,用于找寻数据内在的分布结构,也可作为分类等其他学习任务的前驱过程.例如,在一些商业应用中需对新用户的类型进行判别, {且定义”用户类型”对商家来说却可能不太容易,此时往往可先对用户数据进行聚类,根据聚类结果将每个簇定义为一个类,然后再基于这些类训练分类模型,用于判别新用户的类型.

训练的目标:

1.簇间的距离较大,簇内的距离较小

2.指标和距离公式的选择

性能指标:簇内的相似度和簇间的相似度

3.常见聚类算法

3.1聚类算法类别

类别	典型算法	算法的基本策略
Partitioning approach	K-means,k-medoids,CLARANS,PAM	Construct various partitions and then evaluate them by come criterion
Hierarchical (层次) approach	Diana,Agnes,BIRCH,ROCK,CAMELEON	create a hierarchical decomposition of the set of data(or object) using some criterion
Density-based approach	DBSACN,OPTICS, DenClue	based on connectivity and density functions
Grid-based approach	STING,WaveCluster,CLQUE	based multiple-level granularity (多层次粒度)structure
Model-based	EM,SOM,COBWEB	A model is hypothesized for each of the clusters and tries to find the best fit of that model to each other
Frequent pattern-based	pCluster	based on the analysis of frequent patterns
used-guided or constraint-based	COD(obstacles),constrained clustering	cluster by considering user-specified or application-specifier constraints

4. Partition Algorithm

4.1 k-means

4.1.1算法的基本步骤:

1.创建k个点作为初始质点(经常是随机选取)
2.当任意一个点的簇分配结果发生变化时
			*对于每个数据集中的数据点
					#对于每个质点
							计算出质心与数据点之间的距离
					#将数据点分类到距离最近的簇 
3.对于每个簇,计算簇中的所有点的均值作为新的质心
4.重复上述操作,直至目标函数不再出现更优的结果

目标函数 : 假设 $x_i(i=1,2,…,n)$ 是数据点， $\mu_j(j=1,2,…,k)$ 是初始化的数据中心

$min\sum_{i=1}^n min ||x_i -\mu_j||^2$

这个函数是非凸优化函数,会收敛于局部最优解

函数的曲线如下:[以k=2为例]

4.1.2算法的基本评价

时间复杂度: $O(tkn)$ :t :迭代的次数,k表示类别的个数,n表示样本的数量

相比较 RAM :$O(k(n-k)^2)$ CLARA: $O(ks^2 +k(n-k)$

算法的复杂度比较低,不过很可能得到的是局部最优解(可以通过,模拟退火和遗传算法得到最优解)

缺点: 1. 只能适用于中心值有意义的数据,不适用于categorical data

2.需要提前确定k值

3.因为会出现进入局部最优解的现象,所以会对噪音点,以及最初中心点的设置会很敏感

4. Not suitable to discover clusters with non-convex shapes

4.1.3对于K-means 算法的改进

可以用 modes来代替均值,用其他方法取确定质点
更换其它衡量clusters相似性的标准,处理categorical object---目标函数
using  frequency-based method to update modes of cluster
a mixture of categorical

4.2 K-Medoids

Find representative object,called medoids ,in clusters

4.2.1 PAM

PAM(Partitioning Around Medoids,1987)是作为K-medoids的基础算法,基本流程:

首先随机选择k个对象作为中心
把每个对象分配给离它最近的中心,然后随机地选择一个非中心交替替换中心对象
计算分配后的距离改进量,进而得到改进的cost ,如果cost<0,即结果有改进,则进行交换
直到目标函数不再有改进为止

算法复杂度比较高,只适用于小数据集

4.2.2 CLARA

它从数据集中抽取多个样本集, 对每个样本集使用PAM, 并以最好的聚类作为输出

CLARA 算法的步骤:

　　(1) for 　i = 1 to v (选样的次数) ,重复执行下列步骤( (2) ～ (4) ) :
　　(2) 随机地从整个数据库中抽取一个N(例如：(40 + 2 k))个对象的样本,调用PAM方法从样本中找出样本的k个最优的中心点。
　　(3)对于每个点,把它归类到距离它最近的点的簇
　　(4) 计算上一步中得到的聚类的总代价. 若该值小于当前的最小值,用该值替换当前的最小值,保留在这次选样中得到的k个代表对象作为到目前为止得到的最好的代表对象的集合.
　　(5) 返回到步骤(1) ,开始下一个循环.
　　算法结束后，输出最好的聚类结果

优点:

可以处理的数据集比 PAM大

缺点:

1有效性依赖于样本集的大小

2 基于样本的好的聚类并不一定是整个数据集的好的聚类, 样本可能发生倾斜
　　例如, Oi是整个数据集上最佳的k个中心点之一, 但它不包含在样本中, CLARA将找不到最佳聚类

4.2.3 CLARANS

focusing+spatial data structure

5.层次化聚类方法

一般来说分为两类:

Agglomerative 层次聚类：又称自底向上（bottom-up）的层次聚类，每一个对象最开始都是一个 cluster，每次按一定的准则将最相近的两个 cluster 合并生成一个新的 cluster，如此往复，直至最终所有的对象都属于一个 cluster。这里主要关注此类算法。
Divisive 层次聚类：又称自顶向下（top-down）的层次聚类，最开始所有的对象均属于一个 cluster，每次按一定的准则将某个 cluster 划分为多个 cluster，如此往复，直至每个对象均是一个 cluster。

优点:1 .不需要提前确定k,但是需要一个停止条件

2.可以用树状结构来反映训练的过程,并且得到不同k情况下

的划分方案

缺点: 1

主要思想:

每次找到距离最近的两个点作为一个簇

              2. 把同一个簇的所有点看作一个点
                                             3. 重复上述操作.....直到达到停止条件

5.1 AGNES（Agglomerative Nesting)

sklearn 源码:

1	class sklearn.cluster.AgglomerativeClustering(n_clusters=2, affinity=’euclidean’, memory=None, connectivity=None, compute_full_tree=’auto’, linkage=’ward’, pooling_func=<function mean>)

算法的主要过程:

single linkage: 适用两个簇之间距离最小的一对点的距离作为簇之间的

可以看到，该算法的时间复杂度为 $O(n^3)$ （由于每次合并两个 cluster 时都要遍历大小为 $O(n^2)$ 的距离矩阵来搜索最小距离，而这样的操作需要进行 $n−1$ 次），空间复杂度为 $O(n^2)$ （由于要存储距离矩阵）

5.2 DIANA

是AGNES算法的反过程,最后结果是每个样本都是属于一类

5.3 BIRCH

链接:https://www.cnblogs.com/pinard/p/6179132.html

链接:https://zhuanlan.zhihu.com/p/22458092

5.3.1 CF Tree动态建立的过程:

基本概念:

CF（Clustering Feature）：类簇总体信息三元组 $(N, LS, SS)$ ，其中 $N$ 是一个类簇中数据点个数， $LS$ 是类簇中所有数据点的加和值，即 $\sum_{i=1}^{N}{\bar{X_{i}}}$ ， $SS$ 是类簇中所有数据点的平方和 $\sum_{i=1}^{N}{\bar{X_{i}}^2}$ ，CF相当于对一个类簇的信息做了总结。

性质:

CF可加性定理：

针对两个不相交的类簇，其CF向量分别为 $CF_{1}=(N_{1}, LS_{1}, SS_{1})$ ， $CF_{2}=(N_{2}, LS_{2}, SS_{2})$ ，那么这两个不相交类簇合并后的CF向量为： $CF_{1} CF_{2}=(N_{1} N_{2}, LS_{1} LS_{2}, SS_{1} SS_{2})$ 。这里的证明比较简单，就略去了。
在BRICH中，针对一个类簇，通常只保留其CF向量信息，这样做比较节省空间且高效，后续的聚类需要的计算只需要根据类簇的CF向量即可完成。
CF Tree：类似于B树的一颗高度平衡树，有三个参数：内部节点平衡因子B，叶节点平衡因子L，簇半径T。每个非叶子节点至多包含B个项，形式为 $[CF_{i}, child_{i}]$ ，其中 $child_{i}$ 是指向第i个子节点的指针。每个叶子节点至多包含L个项，且包含指向前后叶子节点的指针prev和next，其中的每一项代表一个类簇，且满足类簇直径小于T。树的结构如下图：

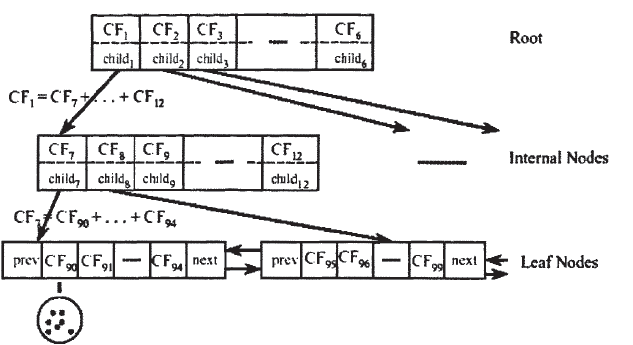
CF Tree会随着新的数据点的加入而动态的建立起来，其插入过程包含以下几步：
（1）从根节点开始，递归向下选择最近的孩子节点，这里最近的度量是根据前面提到的 $D0, D1, D2, D3, D4$ 中任意一个确定；
（2）如果在（1）中找到了最近的叶子节点中的一个 $L_{t}$ ，检查其中最近的CF元组能否不超过阈值T吸收此数据点，若能，更新CF值；若不能，是否有空间（这里每个节点能分配的空间有限，可参见下面的参数表）添加新的元组，若能则添加新的元组，若不能，分裂距离最远的一对元组到两个叶子节点，作为初始的种子，将其他元组按距离最近原则重新分配到两个新的叶子节点上。
（3）从叶子节点向上回溯修改每个非叶子节点的CF值，若叶子节点发生分裂，则在父节点中增加相应的CF元组，同样，父节点也可能需要分裂，则持续分裂直至根节点，最终如果根节点发生分类，则树的高度需要加1。

算法的流程:

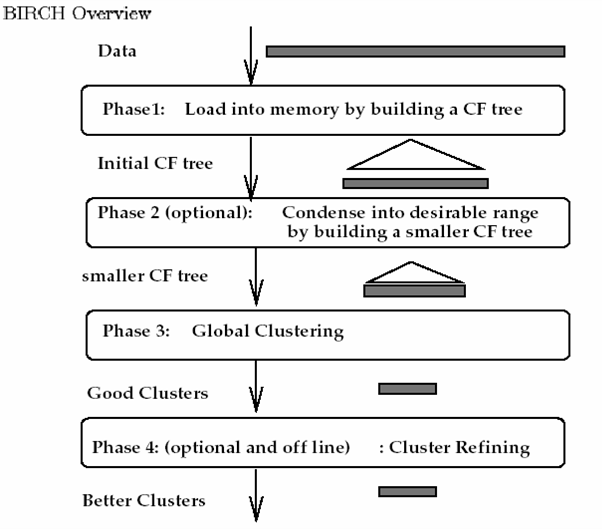
5.3.3算法评价

优点:

1.节省内存 2.速度快 4可以识别噪音点

缺点:

1.结果依赖于数据点的插入顺序

2.对于非球状的簇聚类效果非常不好

3.对于高维数据簇类效果不好

4.局部性可能会导致聚类效果不佳

5.4 ROCK

相似度的计算:jaccard系数,余弦相似度

Jaccard 系数定义为A与B交集的大小与A与B并集的大小的比值，值越大，相似度越高。

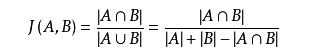
余弦相似度，是通过计算两个向量的夹角余弦值来评估他们的相似度。
值越接近1，就说明夹角角度越接近0°，也就是两个向量越相似，就叫做余弦相似

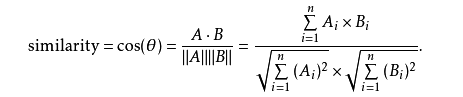
适用于类别型数据,核心思想是利用链接作为相似性的度量,而不仅仅是依赖于距离

clustering categorical data by neighbor and link analysis

5.5 CHAMELEON

https://zhuanlan.zhihu.com/p/55896918

6. 基于密度的聚类算法

“密度聚类” 基于密度的聚类(density-based clustering),此类算法假设聚类结构能通过样本分布的紧密程度确定.通常情况下,从样本密度的角度来考察样本之间的可连接性,并基于可连接样本不断扩展聚类簇以获得最后的聚类结果

主要特点: 1. 可以处理任何形状的cluster

2.可以处理噪音

3.一次扫描

4.需要设置密度参数,作为终止条件

6.1 DBSCAN

参考链接:https://www.cnblogs.com/pinard/p/6208966.html

机器学习–周志华

==一般建议:当数据比较稠密时,而且数据集不是凸的,那么用DBSCAN 会比 K-means聚类效果很好,如果聚类效果不是很好时,不建议用DBSCAN==

6.1.1算法介绍

是基于一组”邻域”(neighborhood) 参数($\epsilon $ ,$MinPts$)来刻画样本分类的紧密程度,

$\epsilon$ 表示了域的半径长度

$MinPts$ :成为核心点的最低密度标准

定义: 给定的数据集$D = { x_1,x_2…x_m }$

所以想要找到满足连接性和最大性的簇的方法就是:如果 $x$ 为核心对象,由 $x$密度可达的所有样本组成的集合$X = { x^{‘} \in D | x_{‘}由x密度可达 }$ 即为满足要求的簇

6.1.2算法的主要流程

I:寻找样本集中所有的核心对象

II:形成满足连接性和最大性的所有核心对象

6.1.3算法小结

　DBSCAN的主要优点有：

　　　1）可以对任意形状的稠密数据集进行聚类，相对的，K-Means之类的聚类算法一般只适用于凸数据集。

　　　2）可以在聚类的同时发现异常点，对数据集中的异常点不敏感。

　　　3）聚类结果没有偏倚，相对的，K-Means之类的聚类算法初始值对聚类结果有很大影响。

DBSCAN的主要缺点有：

　　　　1）如果样本集的密度不均匀、聚类间距差相差很大时，聚类质量较差，这时用DBSCAN聚类一般不适合。

　　　2）如果样本集较大时，聚类收敛时间较长，此时可以对搜索最近邻时建立的$KD$树或者球树进行规模限制来改进。

　　　3）调参相对于传统的K-Means之类的聚类算法稍复杂，主要需要对距离阈值ϵϵ，邻域样本数阈值$MinPts$联合调参，不同的参数组合对最后的聚类效果有较大影响。

6.2 OPTICS

该算法是DBSCAN算法的改进(相关概念延续上面)

6.2.1 定义

说明:如果当x为核心点时,

$$rd(y,x) =\begin{cases} d(x,y) \qquad 当y不是x邻域中的点\ cd(x) \qquad 当y是邻域中的点时,为x的核心距离 \end{cases}$$

https://blog.csdn.net/LoveCarpenter/article/details/85049135

https://bacterous.github.io/2018/01/06/OPTICS%E7%AE%97%E6%B3%95%E5%9F%BA%E7%A1%80/#%E5%AE%9A%E4%B9%89

6.3 DENCLUE

6.4 CLIQUE

7.网格聚类法

STING (a STatistical INformation Grid approach) by Wang, Yang
and Muntz (1997)
WaveCluster by Sheikholeslami, Chatterjee, and Zhang (VLDB’98)

A multi-resolution clustering approach using wavelet method
CLIQUE: Agrawal, et al. (SIGMOD’98)On high-dimensional data (thus put in the section of clustering high-dimensional data

参考链接🔗

https://zhuanlan.zhihu.com/p/104355127